Ich bitte Sie, diese mathematischen Formeln aus Ihrer Sicht zu betrachten und vielleicht eine Erklärung zu geben, wie man diese Gleichung besser oder überhaupt verstehen könnte.
UF#1, UF#2
Die unbekannte mir folgende Formel uF.1 kommt von der Diskussion, die ich mit einem Mitstreiter geführt hatte. Sie resultiert aus meiner Beweißführung, die dem Brief #2 zu entnehmen ist.
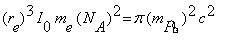
Bild uF.1
die Variablen haben in der Formel folgende Bedeutung:
mPb - Masse eines Bleiatoms in [kg]
re - elektromagnetischer Elektronradius in [m]
me - Masse von einem Elektron [kg]
NA - Avogadro Konstante
I0 - Lichtdruck (Energiedichte) der Sonnenstrahlung auf Orbit von Erde in [N/m2] oder [J/m3].
c - Lichtgeschwindigkeit im Vakuum in [m/s]
UF#2 2 (unbekannte Formel Nr. 2)
aus der gleichen Diskusion:
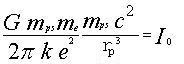
Unbekannte Formel Nr. 2
wo:
mps - die Masse eines Protons (Wasserstoffatoms) [kg]
me - die Masse eines Elektrons [kg]
e – elementare Ladung in [C]
k - Coulomb-Konstante in [V*m /A*s] oder ·[N m2 / C2]
rp - Protonradius oder elementare Einheit von Länge in [m]
Die elementaren Einheiten von Masse, Länge und Zeit (τ) erfühlen folgende Gleichung:
h = mps * rp * c = mps * rp2/ τ
wo:
c - Lichtgeschwidnigkeit in Vakuum
τ = rp / c
Der Multiplikand stellt in der zweiten Gleichung eine elementare Energiedichte
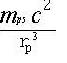
dar und ist gleich: 6,51518111 1034 J/m3
Der Multiplikator in der Gleichung
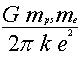
ist gleich: 7,01505092 10-41 und muss nicht kommentiert werden, da er selbsterklärend ist.
Der Produkt den beiden Faktoren ergibt den Wert von I0 auf der Erde mit 4,57 10-6 J/m3.
Berechne ich in der obigen Gleichung die Schwerkrafft zwischen zwei Wasserstoff Atomen, also
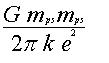
und nehme den Faktor 8 π an, dann ergibt sich die Zahl 0,211 J/m3, was die I0 auf der Sonneoberfläche darstellt.
Warum aber das Ersetzen von Masse eines Elektrons mit der Masse eines Wasserstoffatoms (1836 me) mit dem Multiplikanten 8 π gerade die Energiedichte der Strahlung der Sonne an Sonnenoberfläche ergibt, habe ich keine Ahnung, übrigens, genauso wie für die Formel Nr. 2.
Darunter habe ich die Formeln noch mal dargestellt:
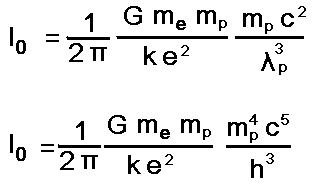
Io - Energiedichte von Sonnenstrahlung auf Erdumlaufbahn.
Anbetracht der folgenden Gleichung:
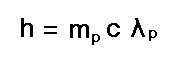
Für Energiedichte auf Sonnenoberfläche:
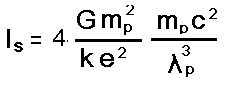
Is - Energiedichte von Sonnenstrahlung auf Sonnenoberfläche