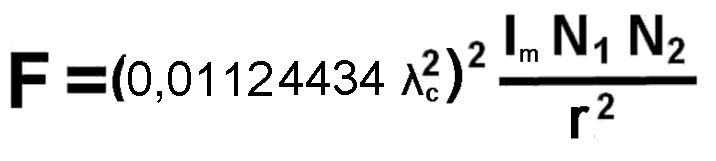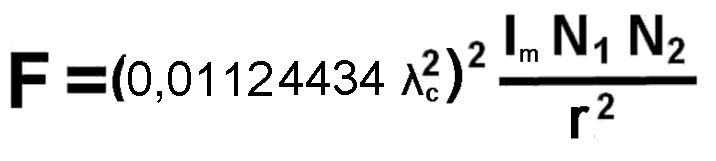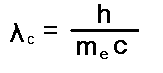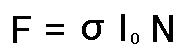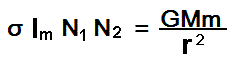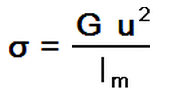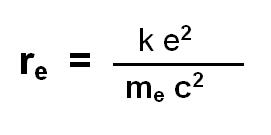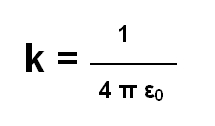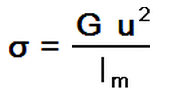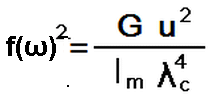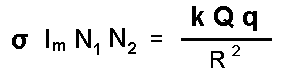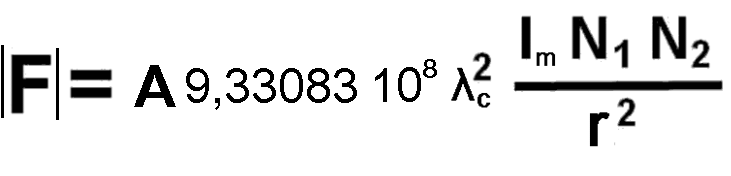Można założyć, że gęstość energii promieniowania
mikrofalowego Im jest jednakowa w całym Wszechświecie, ponieważ
ma ona dużo wspólnego z promieniowaniem reliktowym.
Przypuszczam, że obecnością promieniowania reliktowego można wytłumaczyć
wszystkie rodzaje oddziaływań we Wszechświecie, gdyż to ono
jest za nie odpowiedzialne.
Moja elektromagnetyczna teoria grawitacji może być przypuszczalnie dużo
łatwiej uogólniona do jednolitej teorii wszystkich rodzajów oddziaływań
znanch nam z fizyki, aniżeli inne teorie wymyślone do tej pory.
Nazwałem ją „elektromagnetczną teorą grawitacji“, gdyż wartość
wyrażenia 0,0112... λc2 może przedstawiać średnią
wartość przekroju czynnego na nieelastyczne rozpraszanie mikrofal na
nukleonach w określony przedział kątowy.
Wielkość Im ma wartość gęstości energii fal elektromagnetycznych.
Na podstawie powyższego, nie mam żadnych wątpliwości, że
siła grawitacji jest wynikiem oddziaływania tych fal
elektromagnetycznych z materią.
Pod „stałe fizyczne” podałem wartości wybranych stałych
fizycznych, które użyłem do obliczeń.
15.05.2018
Wzór nr. 1 wyprowadziłem wzorując się na teoretycznym ogólnie znanym
poniższym wzorze, z którym spodkałem się także na
poniższej stronie w internecie przedstawiającej teorię
zaproponowaną przez Steffena Kühna o Quantinos.
Teoria Quantinos.
Zakładam, że źródło promieniowania elektromagnetycznego ( Quantinos
zródło w teorii Kühna), jak np. Słońce lub dowolna masa,
odziaływuje z innymi otaczającymi je ciałami tylko przy pomocy
fotonów.
A więc siła, która działa na ciała, jest niekonicznie
zależna od źródła jakiegoś prominiowania, jeżeli mamy do
czynienia z dużą ilością ciał lub z ciałmi bardzo
odległymi od żródła. W tym przypadku można tę
siłę przedstawić następująco:
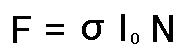
Wzór nr. 0.
Potraktowałem siły na dużych odległościach inaczej (pod (0)) aniżeli
siły oddziaływania na małych odległościach
pomiędzy dwoma ciałami, jak poniżej, gdzie wziąłem pod
uwagę liczbę oddziaływujących ze sobą cząstek N znajdujących
się zarówna w jednym ciele N1 jak i w drugim N2.
F = σ I N1 N2
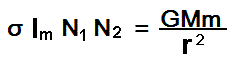
Równanie nr. 1
Z tego równania obliczyłem poniższą wartość.
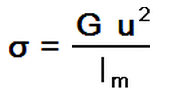
G jest tu wartością stałej grawitacji.
Najczęściej wyrażamy przekrój czynny na jakieś rozproszenie poprzez kwadrat
pewnej określonej długości (odległości), którą to
oznaczamy np. λc oder re i mówimy wtedy o długości fali
Comptona odpowiadającej energii spoczynkowej Elektronu lub o promieniu Elektronu,
który to możemy obliczyć przy pomocy poniższego wzoru:
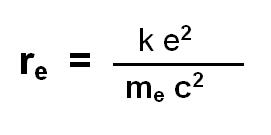
Wzór nr. 2
i:
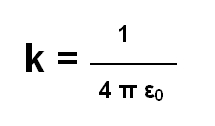
Wzór 3.
k - stała Coulomba w [V*m /A*s]
ε0 - stała pola elektrycznego w [ F / m]
e - ładunek elementarny (ładunek jednego Elektronu) w [C]
me - masa Elektronu w [kg]
re - elektromagnetyczny promień Elektronu w [m]
Przekrój czynny jest zatem iloczynem jednej z tych wielkości λc lub re
podniesionych do kwadratu z pewną funkcją częstotliwości
kołowej ω a więc f(ω).
Można to przedstawić w poniższy sposób:
σ = f(ω) (λc)2 (4)
lub
σ = f(ω) (re)2 (5)
Przekrój czynny jest zawsze zależny od energii cząstek, które ze sobą
oddziaływują w różnych procesach rozpraszania.
Musi on przybierać jakąś wartość średnią,
jeżeli rozpatrujemy rozpraszanie dużej ilości cząstek, które
przenoszą w ten sposób pęd od cząstki na inną
cząstkę lub te prozesy są rozpatrywane w dużym okresie
czasu (odpowiednio dużym do badanego przypadku rozpraszania, czyli rodzaju
oddziaływania).
Z tego powodu σ przybiera pewną określoną
wartość dla określonego rodzaju oddziaływania.
Po uproszczeniach otrzymałem poniższy wzór:
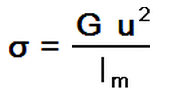
Ten przekrój czynny sigma (σ) jest stały dla wszystkich ciał we
Wszechświecie i wynosi:
σ = 0,43818 10-50 m2
Można tę wartość przedstawić jako iloczyn według formy (4) lub (5).
Zdecydowałem się na użycie wzoru (4).
Wartość σ jest bliska wartości otrzymanej w wyniku podniesienia długości
fali Comptona λc do czwartej potęgi.
λc4 = (2,42631 10-12 m)4 = 3,46564 10-47 m4
I wtedy zachodzi
σ = (0,01124434)2 λc4 = (0,01124434 λc2)2
f(ω)= 0,01124434
Uwzględniając definicję (4) muszę wartość σ podnieść do kwadratu,
ponieważ warość λc występuje tu w czwartej potędze.
Ta zależność pozwala mi na obliczenie funkcji f(ω), jak poniżej:
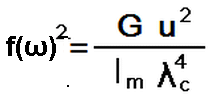
Wzór nr. 6
Powyższa metoda pozwoliła mi też na inne przedstawienie wzoru na siły
elektrostatyczne pomiędzy ładunkami elektrycznymi, jak poniżej.
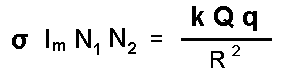
Równanie 2.
Gdzie:
N1 = Q / e
N2 = q / e
Tutaj e oznacza wartość ładunku elementarnego.
Te równanie po przekształceniach można przedstawić jako wzór 7 na siłę Coulomba, jak poniżej,
gdzie A wynosi m2:
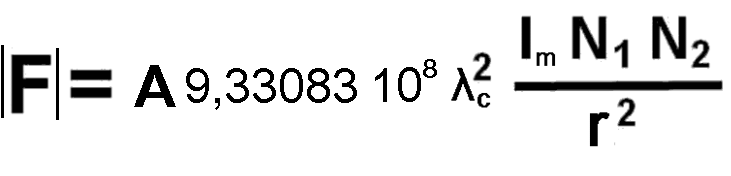
Wzór 7.
Funkcja f(ω) przyjmuje dla oddziaływania elektrostatycznego
poniższą wartość:
f(ω) = 9,33083 108
Można zatem w podobny sposób przedstawić wzorami te dwa rodzaje
oddziaływań i tylko jedno jedyne promieniowanie byłoby
nośnikiem tych obu oddziaływań.
Jest to promieniowanie mikrofalowe, którego temperatura odpowiada prawie
temperaturze promieniowania reliktowego.
Czy można uznać oba wzory jako reprezentację rzeczywistości
tych oddziaływań, czy jest to tylko przypadek?
Zaryzykowałbym doświadczenia badające, czy promieniowanie mikrofalowe ma jakiś
wpływ na wartość siły pomiędzy dwoma ciałami
mającymi jakieś ładunki, ale nie jestem w stanie ich
przeprowadzić.